Blog de RED. Revista de Educación a Distancia. Enseñanza y aprendizaje ayudados por la tecnología. Diseño instruccional y calidad de la enseñanza abierta en línea.
Impact Factor (IF) and Journal Citation Indicator (JCI). CATEGORY EDUCATION & EDUCATIONAL RESEARCH):
2023 IMPACT FACTOR 1,9
2023 IMPACT FACTOR WITHOUT SELF CITATIONS 1,7
2023 Journal Citation Indicator (JCI) 0.84
JIF rank #212/756
Respecto a España y a su posición en Educación e Investigación Educativa
Su posición es #10/73 centil 87%, Q1
50 primeras revistas de Educación e Investigación Educativa ordenadas por JIF y citas
Datos generales
1.142
RED como revista científica de Educación
Índices
RED como revista científica de Computación/Aplicaciones y Computación/;iscelanea: Q2, centil
RED como revista científica de Ingeniería del Aprendizaje e Ingeniería del Conocimiento: Q2 centil
Entre las revistas en cuyo titulo aparece la palabra "educación"
Ayer se publicó el número especial de RED IA generativa, ChatGPT y Educación. Consecuencias para el Aprendizaje Inteligente y la Evaluación EducativaIA generativa, ChatGPT y Educación. Consecuencias para el Aprendizaje Inteligente y la Evaluación Educativa.
En anteriores entradas nos hemos hecho eco de las vicisitudes pasadas, aquí aquí y en RED de Hypoteses
Con aspecto sobrio y denotativo, casi lacónico, como corresponde a la literatura cientifica, aparece nuestro número especial de RED. Está dedicado a la Inteligencia Artificial Generativa y a la Educación.
Nada que ver con las alharacas, los estridentes y llamativos colores y las imágenes de personas jovenes, bien parecidas, sanas y simpáticas con que se anuncia la IA particularmente en la Educación y sus ventaja, que supuestamente la hacen imprescindible para todo.
Ha sido casi un año de intenso trabajo, para sacar con dos meses de anticipación este número monográfico. En su editorial (https://revistas.um.es/red/article/view/609801) pueden leer con detenimiento su historia, un resumen de su contenido y sus conclusiones.
De forma sintética, podemos decir razonadamente que es lo que hay de investigación con evidencias aportadas sobre el tema.
RED es un journal de prestigio y bien posicionado, como lo demuestran las firmas y los artículos que aparecen en él. No es una macrorevista hipercitada, tampoco lo pretende. Huimos de los llamados nefarious numbers, es decir las prácticas que aumentan la citación irrelevante y el impacto, como son las revisiones de la literatura per se y los self report studies.
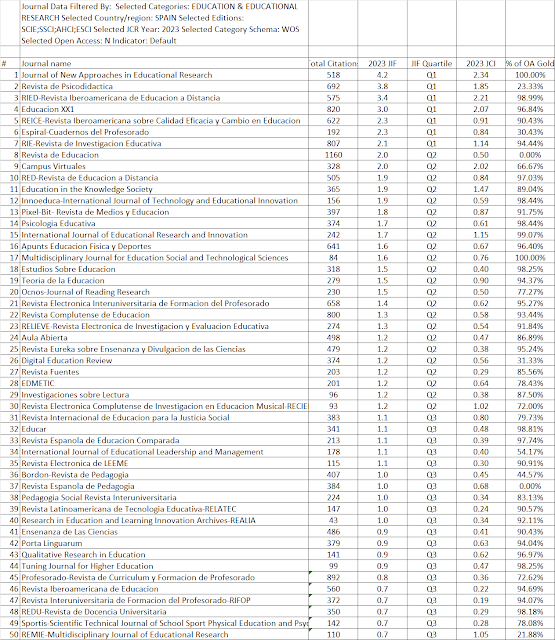
No obstante está en el primer cuartil de Scopus (Q1), en el Q2 de SJR y con un factor de impacto 2.0 en JCR. Esto al menos haría suponer que no desanimaría de publicar aquí por la posición, ANECA la considera muy bien, tanto para la especialidad de Educación como para las otras donde está incluida: Ciencias de la Computación (Aplicaciones y miscelánea) e Ingeniería (considerando miscelánea la ingeniería del aprendizaje y del conocimiento).
Por tanto podríamos descartar una categoria inadecuada como factor de inhibición a la hora de enviar originales.
Tampoco ha sido por falta de plazo. La IA generativa tiene ya tiempo suficiente para haberse experimentado, sobre todo si la comparamos con las ventajas para el aprendizaje que se le atribuyen.
Se dio de plazo desde junio del 2023 hasta el 30 de enero de este año para enviar originales.
Al final solo se han podido publicar SEIS ORIGINALES DE INVESTIGACIONES EMPÍRICAS Y UN ENSAYO. Eso después de haber desestimado más de cien envíos por no ajustarse a lo exigido.
Si se tiene en cuenta el indudable interés de publicar aquí, junto con el plazo dado y lo poco realmente relevante y en consonancia con lo pedido que se ha enviado ¿qué cabe concluir?
¿Seríamos temerarios si dijésemos que es que hay muy poco experimentado?
Desde luego en el área hispanohablante creemos que es así, Y apostaríamos que en el resto, por lo que hemos visto y explicamos en el editorial creemos que también. Ello no excluye el altísimo interés y la calidad de los artículos en inglés, particularmente los del grupo de Dublin, el de Zagreb y el de Polonia. Tamboco se quedan atras las contribuciones publicadas en español por grupos de la UOC, la Universidad de Alicante y la de Salamanca.
La conclusión es que queda mucho por investigar y que buena parte de lo que se dice sobre IA y Educación es pura exegesis o especulación cuando no charlatanería interesada.
Interesada porque hay muchos intereses en juego y grandes recursos puestos en circulación. Hace unos días un interesante artículo de The Economist lo decíaun interesante artículo de The Economist lo decía.
Desde la academia y la investigación educativa seguiremos en esta línea.
Acontinuación reproducimos íntegra la presentación del número, de cuyos preprints pueden tener versiones en EdArXivEdArXiv y en ResearchGateResearchGate
El 1 de julio de 2023, haciéndose
eco del auge de un Modelo de Lenguaje Grande LLM (Large Language Models)
conocido como ChatGPT, la Revista Educación a Distancia abrió el plazo para
enviar contribuciones a su número especial sobre IA generativa,
ChatGPT y Educación, donde se presta especial atención a sus consecuencias para
el aprendizaje inteligente y la evaluación educativa.
En este monográfico, se quería
dar espacio a contribuciones que incluyesen investigación relacionada con la
IA, ChatGPT y sistemas transformadores LLM y educación. Y también a
experiencias sobre el aprendizaje inteligente y evaluación formativa en contextos
ChatGPT. Un año después publicamos este número.
En esta presentación queremos
recordar los motivos que nos llevaron a la convocatoria y los resultados
obtenidos, relacionándolos con los objetivos que nos propusimos
Justificación:
Para esta convocatoria se
tuvieron en cuenta, entre otras, las siguientes razones.
Hace un año percibíamos que una
modalidad de inteligencia artificial (IA) se había impuesto, al menos teniendo
en cuenta lo que dicen los medios, y avanza rápidamente. Aunque las cosas
cambian en nuestra historia mundial y quizá la dirección de la IA cambie en un
momento no muy lejano. Así, por ejemplo, otras modalidades anteriores, como era
la basada en la programación declarativa y en la programación lógica cayó hace
mucho en desuso.
En ese sentido, no sabíamos y
seguimos ignorando por qué entre las dos formas posibles de simular un cerebro
humano, como las que expresa por Noam Chomsky (2023) en el párrafo siguiente y
la IA generativa, se ha optado en apariencia por la segunda. Aunque nosotros no
damos por cerrada la disyuntiva, sobre todo antes de debates como éste o de las
prácticas e investigaciones que se produzcan.
Veamos cual es la apuesta de
Chomsky que siempre tiene el encanto de la frescura de quien habla con
desparpajo en función de su profundo conocimiento de la inteligencia natural en
el ámbito de lo generativo como marco para inscribir el desarrollo del
lenguaje:
La mente humana no es, como ChatGPT y sus
similares, un pesado motor estadístico para la coincidencia de patrones, que se
atiborra de cientos de terabytes de datos y extrapola la respuesta
conversacional más probable o la respuesta más probable a una pregunta
científica. Por el contrario, la mente humana es un sistema
sorprendentemente eficiente y hasta elegante que opera con pequeñas cantidades
de información; no busca inferir correlaciones brutas entre puntos de
datos, sino crear explicaciones.
Por ejemplo, un niño pequeño que adquiere
un idioma está desarrollando —inconsciente, automática y rápidamente a partir
de datos minúsculos— una gramática, un sistema extraordinariamente sofisticado
de principios y parámetros lógicos[1].
Pero ésa ha sido la elección y
tras décadas de investigación y de desarrollos, en esta fase se ha decidido por
parte de OpenAI, y después por otras empresas, que este tipo de IA pase de los
laboratorios a la aplicación práctica en la sociedad. No sabemos si ha sido
efecto de estímulos de estrategias empresariales y económicas, siempre
difíciles de discernir, o porque la sociedad lo ha aceptado así como
consecuencia de dinámicas evolutivas, pero el hecho es que se ha producido un
colosal despliegue de la IA generativa.
La educación no ha sido
indiferente a esa aceptación ni a ese despliegue.
En esta situación, hasta donde se
ha dicho (Dawson, S., Joksimovic, S., Mills, C., Gašević, D., & Siemens,
G., 2023), el mundo de la educación se enfrenta a dos posibles dinámicas con
diferentes resultados, según nuestro análisis de hace un año.
En primer lugar, los que se
derivan de que la IA tiene el potencial de revolucionar los métodos de
enseñanza, la evaluación y la ayuda al alumno, existentes. De lo primero y
lo segundo hablaremos después
En segundo lugar, según estos
mismos autores y lo que parece ser un sentir común, la IA también tiene la
capacidad de crear un sistema educativo completamente nuevo. Y se cita
como justificación que el pensamiento creativo y la resolución de problemas son
fundamentales en entornos modernos y muy complejos. Y esta IA podría
ayudar a los alumnos a enfrentarse a esos problemas. Aunque esto es lo que
dicen estos autores y en el trasfondo de esta cuestión siempre tendríamos que
tener en cuenta que las tecnologías han sido frecuentemente sobrestimadas desde
su principio como fuente de cambio de paradigma educativo en los sistemas
escolares (expectativas con videodisco
interactivo, pizarra digital, e incluso la educación virtual en la pasada
pandemia como algo sin punto de retroceso, o recientemente ha sucedido con el
metaverso (ver nuestro número especial Visiones de espacios de trabajo
tridimensionales o virtuales y educación) pero que aún ese nuevo
paradigma exclusivamente basado en la tecnología no ha emergido, aunque sí haya
autores que muy razonadamente han planteado que asistimos a un cambio de
paradigma cultural decisivo que influye en la educación (Reigeluth, 2016) (Zapata-Ros,
febrero 2014).
Estas tres cuestiones ya por
sí solas planteaban tres desafíos y otros tantos ejes de posibles para
investigaciones y contribuciones.
Esto lo planteábamos
pensando positivamente. Pero había otras cuestiones que podían ser planteadas
en sentido negativo o como interrogantes:
¿Cuáles son los impactos que
se producen cuando la IA comienza a servir como un socio (¿cabría decir “servir
como socio”, o más bien “ser socio” o, por el contrario, “servir como
herramienta”?) activo en acciones sociales, creativas e intelectuales sostenidas,
no sólo puntuales o como repuesta a preguntas aisladas. Ahora esos impactos en
las prácticas que puedan existir son desconocidos. Ya hemos dicho que
indagar esas prácticas también puede ser objeto de contribución.
Entre
esos rasgos y sus correspondientes prácticas[2] se incluyen a bote pronto la
autorregulación (Zapata-Ros, 2015, 2013)(Reigeluth, 2016)(Huh
& Reigeluth, 2017) (Garello
& Rinaudo, 2013), la metacognición (Huh & Reigeluth, 2017) (Reigeluth,
2006), la orientación a objetivos, la planificación, las tormentas de ideas
creativas y una variedad de habilidades que podrían verse afectadas
negativamente por la automatización o la toma de control de las máquinas.
Paradójicamente
estos rasgos a más de ser humanos son constitutivos de lo que se ha llamado
pensamiento computacional (Wing, 2008)(Grover & Pea, 2013)(Zapata-Ros, sept
2015), de manera que un uso no controlado podría derivar en una nula o una mala
adquisición de ese tipo de pensamiento que hoy se considera constitutivo de una
nueva alfabetización en la sociedad digital (Zapata-Ros, sept 2015)
En
particular, para la metacognición, la autorregulación y retroalimentación
podemos citar:
Hilpert et al. (2023) abordan la
necesidad de participación en el aprendizaje de STEM, con una mayor necesidad
de autorregulación de los estudiantes. Se basan en una extensa historia de la
ciencia de la investigación del aprendizaje que utiliza datos de seguimiento
digital para crear construcciones cognitivas que brindan información sobre el
compromiso, las redes sociales, la comunidad y la metacognición. En este
documento, detallan la importancia de la regularidad de la participación como
un fuerte predictor del resultado del curso y los efectos del uso de una
intervención de la ciencia de aprender a aprender para fomentar el SRL de los
estudiantes y la participación continua. Sus resultados sugieren efectos
prometedores y sostenidos de este entrenamiento, lo que plantea la necesidad de
considerar enfoques teóricos que integren las observaciones del comportamiento
con las construcciones cognitivas en la educación digital.
Bauer et al. (2023) abordan un área
crítica de aprendizaje relacionada con la retroalimentación. La
retroalimentación es fundamental para guiar el progreso de los estudiantes y
los enfoques tradicionales se basan principalmente en la observación humana.
Sin
embargo, el mismo autor, señala un posible progreso del que después hablaremos, cuando lo
hagamos de aprendizaje inteligente como aprendizaje inclusivo:
Con el desarrollo de grandes modelos de
lenguaje y el procesamiento del lenguaje natural en general, existen nuevas
oportunidades para ofrecer retroalimentación a los estudiantes. Detallan cómo
los artefactos textuales pueden mejorarse con la retroalimentación de la IA.
Ofrecen un marco para conectar los procesos de retroalimentación con el apoyo
estudiantil adaptativo. A medida que el aprendizaje digital crece en
importancia en los entornos educativos, la inclusión de artefactos más diversos
y multimodales requerirá una actualización similar de la teoría y las
construcciones para garantizar la retroalimentación como motor del éxito
general de los estudiantes.
Una pedagogía y una teoría del aprendizaje de la IA
Para abordar estas preguntas y en
general la necesidad de un despliegue efectivo de los sistemas de IA en la
educación, es preciso hacerlo desde un punto de vista teórico, más allá de los
resultados que sobre las interrogantes señaladas, nos proporcione la
investigación empírica, que no guíe y dirija en nuevas rondas, tanto en la
investigación como la práctica.
Ese marco teórico, suponíamos
entonces, nos proporcionará los asideros y las andaderas para garantizar que
los principios, los valores y las construcciones confiables configuren el uso
de la IA en la educación. De esta forma, nos aseguramos de que los valores, la investigación
realizada hasta ese momento, los intereses y preocupaciones de las partes
interesadas y las contribuciones que se vayan haciendo sigan integrándose de
forma cohesionada en el escenario de la IA en la educación. Al menos como deseo
y horizonte.
En las conclusiones veremos
en qué escasa medida estas expectativas se han cumplido. Como consecuencia, lo
que veíamos como una necesidad en esta convocatoria: la importancia crítica de
la teoría en el diseño, desarrollo y despliegue de la IA en la educación se ve
necesaria ahora, así como la creación de una nueva sección de RED. En esa
perspectiva, nos planteamos de forma crítica la relevancia y la continuidad de
las teorías de aprendizaje ya existentes cuando la IA se constituya como una
realidad en las aulas.
También reiteramos, por
incumplida, la llamada a considerar nuevos marcos, modelos y formas de pensar.
Nos referimos a aquellos que incluyen la presencia de agentes no humanos,
que dudamos en llamar una nueva tecnología, porque se parece más a un socio
activo que a una tecnología simple, como sucedía hasta ahora. Ello incluso en
el caso de que hablemos de la tecnología digital, que respondía más a
interrogantes lógicas simples que a un agente con capacidad para tomar
decisiones intermedias sin intervención humana, del alumno o del profesor.
Cabe ahora hablar de un
trinomio, más que de un binomio. Situación que requiere como hemos dicho nuevos
marcos, modelos y formas de pensar.
Ese planteamiento, siguiendo
con las primeras conclusiones de insuficiencia en la respuesta, es precisamente
lo que nos hace insistir en una serie de preguntas importantes para esta
convocatoria, precisamente sobre la revisión de las teorías de aprendizaje
basadas en las configuraciones existentes. Y cuáles serían en este caso
sus alternativas.
Señalábamos que el uso de la
teoría en la investigación educativa constituía la lente a través de la que
vemos y explicamos lo que observamos (Biesta et al, 2011).
¿Pero es útil la lente que tenemos hora?
Las teorías existentes se
establecieron y se derivaron de un contexto educativo distinto al de los
enfoques de enseñanza más recientes y al de los sistemas tan fuertemente
apoyados por la tecnología. Es de prever más aún que a medida que la
adopción de la IA impacte en la enseñanza y el aprendizaje, se produzcan dudas
la idoneidad en continuación de las teorías de aprendizaje existentes.
Sin embargo, como dijimos,
la integración del desarrollo e implementación de sistemas educativos basados
en IA en marcos teóricos adecuados es esencial para avanzar y lograr
resultados de aprendizaje óptimos. En base a estas ideas, planteábamos las
siguientes interrogantes:
¿La integración de la IA en
la educación requiere modificaciones o revisiones en la forma en que
aprendemos?
¿O, por el contrario, se
requiere una reestructuración completa, lo que conlleva la necesidad de nuevas
teorías?
¿Qué debería ofrecer la
teoría a los educadores cuando se incluye la IA?
Con relación al modo en que
se persiguen y abordan estas cuestiones, nos planteamos:
En los programas LLM, la facilidad de acceso a los contenidos y la capacidad de
producirlos, ¿disminuyen la importancia del conocimiento declarativo?
Se habló mucho del
constructivismo social vinculado al aprendizaje apoyado por las tecnologías
digitales y sociales. Del mismo modo podríamos plantear si ¿los puntos de vista
existentes sobre el constructivismo social avalan la IA como un agente social en
el aprendizaje?
También podríamos hacer
incursiones microteóricas. Como, por ejemplo, plantearnos si los corpus
teórico-prácticos existentes ¿sirven suficientemente, o son los adecuados, para
la inclusión de la IA en las aulas o es necesario actualizarlos o incluso
repensarlos por completo?
Aprendizaje inteligente
En la llamada a
contribuciones también hablamos del llamado aprendizaje inteligente, como fase
más avanzada del aprendizaje adaptativo.
Decíamos que, si bien el
debate suscitado en este número especial podría, en alguna medida, servir para
orientar la investigación en torno a la nueva visión que se abre con la IA
generativa, hay unos planteamientos anteriores que hemos citado en otras
ocasiones y que no conviene olvidar: Es la consideración del llamado
aprendizaje inteligente (Zapata-Ros, 2018) (Hwang, 2014) como una fase superior
del aprendizaje adaptativo.
Así, decíamos que el
constructo de "entornos de aprendizaje inteligentes" se había
establecido a partir
de la definición
de Hwang (2014),
como entornos de
aprendizaje apoyados por la
tecnología que realizan
adaptaciones y brindan
el soporte adecuado
con la tecnología de
detección y de
recomendación (por ejemplo,
orientación, retroalimentación,
consejos o herramientas)
en los lugares
adecuados y en
el momento oportuno,
según las necesidades individuales
de cada alumno, determinados
mediante el análisis de sus comportamientos de aprendizaje, su trayectoria de
rendimiento y los contextos en línea y del mundo real en los que se encuentran,
tanto grupales y sociales como
compuesto por los recursos de que se provee o a los que
accede, descarga, lee o elabora.
Y que el aprendizaje
inteligente podría considerarse consecuentemente (Zapata-Ros, 2018) como aquel
aprendizaje que pueden desencadenar y producir los sistemas de aprendizaje
inteligente, y que se puede entender de forma diferenciada por las funciones y
efectos que no se pueden realizar en ambientes de aprendizaje adaptativo y de
aprendizaje contextualizado, sin excluirlas. El aprendizaje social y el
aprendizaje colaborativo de esta forma se puede entender como una subcategoría
del aprendizaje contextualizado.
Resumiendo, se puede decir
pues que el aprendizaje inteligente es el aprendizaje adaptativo y
contextualizado con mecanismos de detección, de respuesta y de recomendación.
Entonces (Zapata-Ros, 2018) se planteaba:
La presencia y el avance de las tecnologías de detección
y de recomendación están ofreciendo grandes y determinantes oportunidades para
desarrollar nuevos entornos de
aprendizaje. Definitivamente el aprendizaje inteligente es un concepto
extremadamente innovador, como en otros ámbitos, para desarrollar visiones
y planteamientos distintos. En este caso para crear entornos de aprendizaje
más potentes y
útiles que los enfoques
de aprendizaje ayudados por
la tecnología ya
existentes, mediante la
incorporación de nuevas herramientas y nuevos criterios para
el aprendizaje.
La cuestión ahora sería: aquello
que se abrió como un desarrollo del aprendizaje adaptativo y cuyas primeras y
muy contadas experiencias en relación con la Educación Superior se vieron en el
artículo citado (Zapata-Ros, 2018), cuál es su estado ahora, qué experiencias y
qué conclusiones se han obtenido de las investigaciones en esta línea no sólo
en la Educación Superior, si es que las ha habido, y finalmente cuál es su
estado y cuáles son sus perspectivas en relación con la IA de nuevo cuño, la de
los sistemas generativos.
Por zanjar la cuestión y
centrarnos en la otra, podemos decir que el monográfico no ha avanzado nada en
esta línea, al menos en el limitado campo de nuestra convocatoria. Lo cual no
excluye que se hayan obtenido por otro lado. Sin embargo, hay que decir que,
entre las revisiones de la literatura recibidas, que en este caso hubiéramos
aceptado a pesar de la política de nuestra revista, no ha habido ninguna sobre
el aprendizaje inteligente así considerado.
Resumiendo, con este
monográfico, se ofrecía un espacio para contribuciones que esencialmente
incluyan investigaciones empíricas y/o el desarrollo y prueba de una o más
tecnologías en relación con los LLM generativos, estudios de casos o
desarrollos teóricos[3]
sobre aprendizaje con IA, ChatGPT y sistemas transformadores LLM y Educación.
Finalmente se han publicado seis
contribuciones, incluyendo el ensayo de uno de los editores invitados, que
pasamos a resumir, pero que, en todo caso, han dado respuestas muy limitadas a
lo planteado. Respuestas que iremos respondiendo en el contexto de las
resumidas reseñas que hacemos.
Resultados
Hay propiamente seis
investigaciones empíricas y un ensayo.
Entre las investigaciones
empíricas reseñamos en primer lugar la de Machine vs Machine: Large Language
Models (LLMs) in Applied Machine Learning. High-Stakes Open-Book Exams (Quille
et al., 2024).
Se trata de un estudio muy
focalizado en una forma de evaluación, la de
exámenes supervisados con libros cerrados y abiertos, que hace
longitudinalmente a lo largo de seis años, y la comparación con los resultados
colaborativos de profesores y alumnos utilizando LLM.
Este artículo tiene como
objetivo abordar una brecha notable que los autores han encontrado dentro del
campo de la investigación en Educación en Computación (Computing Education
Research CER) al investigar el impacto de los Modelos de Lenguaje Grande (LLMs)
en educación superior, específicamente en una asignatura de grado de Applied Machine Learning, en el último año
en varios entornos de examen. Es un estudio semilongitudinal. Obtiene los
resultados de exámenes supervisados con libros cerrados y abiertos, a lo largo
de seis años, y compara su rendimiento con la eficacia de los LLMs para
responder preguntas sobre los mismos temas. Para ello emplean diversos
formatos, incluyendo preguntas abiertas, basadas en datos tabulares y basadas
en figuras.
Además, el artículo
profundiza en un análisis a nivel micro, identificando preguntas específicas de
examen y tipos de preguntas donde los LLM demuestran grados variables de
eficacia. Explora las herramientas de detección para el contenido generado por los
LLM, examinando su efectividad en identificar salidas originales de esto
programas y aquellas manipuladas por estudiantes. Se trata con ello de obtener
resultados prácticos para mantener la integridad académica.
La pregunta que nos hicimos
es ¿por qué es un estudio secuencial de seis años cuando ChatGPT es de 2022 y
Bing Copilot es de 2023?
Como respuesta obtuvimos que el objetivo de esta
investigación es abordar y comprender la efectividad y el uso de los LLM para
responder preguntas de exámenes a libro abierto y cerrado. Durante las
reuniones del equipo se establecieron criterios para evaluar los objetivos de
la investigación. El proceso de colaboración entre estudiantes y personal
académico implicó experimentar con varios LLM y diferentes entradas para
definir criterios de evaluación e identificar detectores de LLM adecuados. El
análisis se aplicó a un conjunto de datos que, procedentes de los exámenes,
abarca seis años de las pruebas escritas de la asignatura Aplied machine
learning. Luego, después en la época que ya existen los LLM, se utilizó la
base de datos de BSc. (Honours) Computing programme para comparar los con los del
desempeño del LLM para diferentes formatos de exámenes y tipos de preguntas
procedentes de los exámenes, proporcionando una base integral para el análisis
y la discusión.
Para esta parte del estudio
se utilizaron varios LLM y versiones de LLM, incluidos ChatGPT 3.5, ChatGPT 4 y
Bing Chat.
Otro objetivo de
investigación es evaluar la efectividad de los detectores de LLM usados,
eventualmente con propósito de fraude, para resultados de LLM sin procesar y
resultados de LLM manipulados por los estudiantes. Tanto en la salida original,
inalterada, de los LLM como en la salida manipulada. El resultado manipulado es
cuando los estudiantes modificaron la respuesta del resultado LLM a una
pregunta, en un esfuerzo por ocultar esto para que no fuera detectado. El
estudio evalúa el rendimiento de estos detectores en la salida directa de LLM,
así como en el contenido generado por el modelo de lenguaje manipulado por los
estudiantes. Además de esto, el estudio examina el desempeño del LLM al
distinguir entre contenido generado por modelos de lenguaje auténtico y
manipulado.
Resultados y conclusiones
Si bien puede que no sea tan
sorprendente, los LLM como estudiantes superaron con creces a los estudiantes
en todos los exámenes tanto de libro abierto como a libro cerrado. Esto no es
demasiado sorprendente ya que los estudiantes están limitados por sus
conocimientos y habilidades técnicas y, a veces, por su capacidad para aprender
de memoria. Dado que los LLM tienen esta capacidad de superar a los estudiantes,
los educadores deben tener cuidado con el tipo de preguntas que se hacen.
En el análisis de las
respuestas a las preguntas, el principal tipo de preguntas que resultaron ser
un obstáculo para los tres LLM fueron las preguntas que incluían imágenes.
Se produjo un patrón
razonablemente consistente en el que Bing reconocía que no podía ver las
imágenes, generalmente afirmaba algo como: “Sin más información sobre el
histograma, es difícil describirlo” y no daba más información. ChatGPT 3.5 hacía
una de dos: en aproximadamente el 25% de los casos, fabricaría valores
numéricos y respuestas que eran completamente incorrectas, y en el 75% de los
casos diría algo como lo siguiente: "Lo siento, pero no puedo ver el
histograma al que te refieres”, y luego proporcionaría algunas instrucciones
genéricas ampliamente relevantes para la pregunta. Finalmente, ChatGPT 4
normalmente diría algo como lo siguiente: "Pido disculpas, pero no puedo
ver el histograma al que te refieres en tu pregunta" y proporcionaría
algunas instrucciones genéricas que eran directamente relevantes para la
pregunta.
Sin embargo, en todas las
preguntas que tienen histogramas, había una tabla adjunta que resumía algunas
estadísticas clave asociadas con ese histograma, y esa tabla de resumen a veces
era parte de la imagen, pero a veces era una tabla adjunta basada en texto. En los casos en que la tabla estaba basada en
texto, los LLM pudieron hacer inferencias sobre el histograma (como su
inclinación) que los hacía parecer como si pudieran ver las imágenes; por lo
tanto, es mejor si todas las tablas adjuntas son imágenes, en lugar de estar
basado en texto. Otro ejemplo interesante de este fenómeno fue evidente en una
pregunta que se vio en varios de los exámenes de Libro Abierto, donde la
pregunta presentaba una imagen de diagrama de dispersión y se pedía discutir el
tema de los datos faltantes "usando el ejemplo de la Figura 1 (o cualquier
otro). otro ejemplo adecuado)”. En casi todos los casos, esto parece haber
confundido a los LLM, que no pudieron tener en cuenta las instrucciones entre
paréntesis y, en cambio, recurrieron a respuestas extremadamente genéricas.
Esto resalta la importancia de cómo se presenta una pregunta; Parece que la
combinación de la imagen como parte de la pregunta y la fraseología particular
en este caso fueron suficientes para confundir significativamente a los LLM en
comparación con los estudiantes, e incluso podría ser el factor decisivo para
el éxito de los estudiantes.
El otro tipo principal de
preguntas que constantemente obstaculizaban los tres LLM eran las que contenían
una tabla de valores. Si se les pidiera que realizaran cálculos en una tabla de
valores, los LLM tenían dificultades, incluso si sabían la fórmula correcta a
aplicar. Pero aun así la aplicaban a los valores incorrectos en la tabla.
Estos casos investigados
arrojan unos resultados a tener en cuenta tanto en la evaluación como a la hora
de diseñar procesos de instrucción y de evaluación, tanto que contengan LLM
explícitamente como en aquellos que los estudiantes los usen, sin estar contemplado
su uso, en el caso general. Esto está dicho a modo de ejemplo, es interesante
leer el artículo completo.
En el trabajo Análisis
mediante inteligencia artificial de las emociones del alumnado autista en la
interacción social con el robot NAO, de Gonzalo Lorenzo Lledó et al (2024),
el objetivo de la investigación es “explorar el uso integrado de la robótica y
la IA para favorecer la comunicación e interacción social en el alumnado con
autismo, analizando las emociones que manifiestan en las actividades diseñadas.
Para ello, se implementó un estudio piloto con el robot NAO y cuatro niños
autistas que desarrollaron actividades de imitación, juego e interacción
social. Durante su realización se utilizó un sistema automático basado en redes
neuronales convolucionales para detectar los estados de ánimo en el proceso de
interacción. Los resultados muestran que tristeza, felicidad y enfado son las
emociones que tiene una mayor probabilidad de producirse en los participantes.
Por tanto, se concluye que el robot y el sistema de inteligencia artificial son
un elemento fundamental para ayudar a expresar sus emociones en las interacciones
sociales”.
Por otro lado, el artículo de Guàrdia, Maina,
Cabrera y Fernández-Ferrer (2024), sobre la autorregulación del aprendizaje
desde un enfoque de feedback entre pares, presenta una investigación que
consideramos muy relevante sobre el tema, desde una perspectiva en principio distinta,
pero con fuertes repercusiones en la IA generativa, y que se articula en el
marco de un proyecto I+D.
Quisiéramos destacar el valor de este trabajo
para el monográfico porque, si bien cuando se diseñó la intervención y se
implementó todavía no se utilizaban de forma tan extensiva los modelos de
lenguaje generados por la Inteligencia Artificial Generativa, al utilizar un chatbot y el feedback entre pares como
apoyo a los procesos de autorregulación e implementar un enfoque de
investigación basado en el diseño, las diferentes iteraciones que se llevaron a
cabo sí que permitieron identificar criterios sobre cómo implementar en una
nueva iteración el uso de IA generativa como asistente para promover una
autorregulación más eficiente.
Es precisamente en este
punto donde está la aportación de la investigación, ya que el artículo sugiere
recomendaciones sobre cómo integrar la IA generativa desde un diseño de
intervención que apoye los procesos de escritura de ensayos académicos del estudiantado,
así como asistir al estudiantado en los procesos de elaboración y reelaboración
del feedback entre pares. Con ello se pone de manifiesto la necesidad de
intensificar estas estrategias para su adecuado desarrollo, aprovechando el
potencial de la IA como apoyo para obtener mejores resultados.
En el trabajo The use of
social robots as teaching assistants in schools: implications for research and
practice de Ružić y Balaban (2024), como en el caso del artículo de Lorenzo
Lledó et al (2024), el protagonista es NAO. La conclusión ahora es que, en los
robots sociales, la IA se ha integrado perfectamente para permitirles
programarse con objeto de realizar una amplia gama de tareas, desde movimientos
e interacciones básicos hasta funciones más complejas, como ayudar en la
educación a la consecución de aprendizajes específicos de repaso y ejercitación.
De esta forma el artículo analiza
y profundiza en el uso multifacético de los robots sociales en la educación
primaria y secundaria, abordando aspectos clave como tendencias, fundamentos
teóricos, dominios de aplicación y consideraciones éticas.
El trabajo está guiado por
cuatro preguntas de investigación
Pregunta 1: ¿Cuáles son las tendencias de
investigación en torno a los temas asociados con la investigación sobre robots
sociales en las escuelas primarias y secundarias?
Pregunta 2: ¿En qué modelos teóricos se basan los
estudios?
Pregunta 3: ¿Cuáles son los dominios de
aplicación en el contexto de los robots sociales en las escuelas primarias y
secundarias?
Pregunta 4: ¿Qué cuestiones
éticas y de privacidad de datos se plantean?
De ellas se constata que el
robot NAO aparece de manera destacada en entornos educativos, particularmente
entre los niños en edad de escuela primaria. Los dominios de aplicación
explorados que se detectan incluyen el aprendizaje de idiomas, el pensamiento
computacional, el desarrollo social y emocional, el apoyo a la creatividad, la
práctica de instrumentos musicales y las actividades de la biblioteca. Mostrando
las diversas funciones que se desempeñan como asistentes de enseñanza, pares y
acompañantes.
Sin embargo, se detectan
preocupaciones éticas y problemas de privacidad de datos. Ello plantea riesgos
como problemas con la transparencia, dependencia humanos con robots,
interacción humana reducida y posible desplazamiento laboral.
Por último, el estudio
enfatiza, y esto es la conclusión más importante, la necesidad de realizar
estudios longitudinales extensos y esfuerzos de colaboración para integrar
responsablemente los robots sociales en la educación, enfatizando la necesidad
de colaboración entre educadores, formuladores de políticas, desarrolladores y
expertos en privacidad para establecer pautas claras que prioricen el bienestar
de los estudiantes.
El trabajo de Hernández-León y
Rodríguez-Conde (2024), Inteligencia artificial aplicada a la educación y la
evaluación educativa en la Universidad: introducción de sistemas de
tutorización inteligentes, sistemas de reconocimiento y otras tendencias
futuras, en principio iba a ser
rechazado en la fase de revisión editorial porque en este número especial no se
aceptaban revisiones de la literatura. La razón era clara: no había una masa
crítica de análisis empíricos que justificase una revisión (Zapata-Ros, diciembre
2023). Finalmente fueron distintas las razones para no hacerlo. Primero, el
trabajo no se refería a IA generativa exclusivamente, trataba “la literatura
existente en Scopus analizando la aplicación de la IA en la educación y la
evaluación de resultados de aprendizaje en la Universidad, en la última década”. Y segundo, existía el precedente y el
paralelismo del trabajo de Siemens y otros en A meta systematic review of
artificial intelligence in higher education: a call for increased ethics,
collaboration, and rigour (Bond, M et al, 2024), en la revista Educational
Technology in Higher Education (ETHE). Aunque en este caso el trabajo
se incluye en la modalidad de “revisión meta sistemática” (meta systematic
review). Esta revisión de revisiones es la primera meta revisión integral
que explora el alcance y la naturaleza de la investigación de AIEd en la
educación superior (AIHEd), mediante la síntesis de investigaciones secundarias.
La diferencia es que en éste caso el análisis intentaba encontrar tendencias a
partir de las revisiones y no sólo de las investigaciones empíricas. El hecho
de que se utilice en este momento, y atraiga la atención, pone de relieve como
ya hemos señalado la ausencia de investigaciones directas que evidencien el
impacto de la genAI en el aprendizaje y por extensión en la educación. Y
en éste, en el que reseñamos, se realiza un análisis sistemático de la
literatura existente en Scopus analizando la aplicación de la IA en la
educación y la evaluación de resultados de aprendizaje en la Universidad, en la
última década.
Como
en aquel trabajo, se señala que la IA que se ha aplicado o se intenta aplicar a
la educación no es sólo la de ahora, que existe un corpus empírico-teórico
desde al menos la década de los setenta del siglo pasado con tendencias y
taxonomías de casos que se señalan en la tabla 2 (página 6) del artículo
reseñado y en el trabajo de Bond et al (2024) en la figura 1.
En
particular, y con referencia a lo que justifica el título del monográfico sobre
la evaluación, el trabajo establece algunas conclusiones interesantes.
Los
resultados han destacado algunos avances en la introducción de sistemas de
tutorización inteligentes, sistemas de reconocimiento para identificar al
discente en formación online, sistemas de seguridad en los diseños del campus
inteligente, la personalización de la educación y algunas tendencias futuras,
como la realidad virtual y aumentada combinada con IA. También en cuestiones
éticas en el uso de la IA.
Concluye
que:
La evaluación
educativa universitaria se va a enfrentar a grandes desafíos a superar, como
son: la creación de normativa específica en el uso de la IA en el ámbito
educativo, la seguridad y privacidad de los datos, los accesos no autorizados a
los datos, el plagio e integridad académica y la integración de los procesos
administrativos de evaluación educativa dentro del sistema de gestión integral
en el contexto del “campus inteligente”.
Otra aportación es
conocer el estado del arte de la evaluación educativa universitaria. Para, en
base a ella, dar a conocer cómo se está perfilando a nivel tecnológico la
evaluación educativa universitaria y los avances que ha habido en la última
década sobre la evaluación integrada en sistemas con IA.
Como hallazgos más
interesantes destacan que:
La evaluación
educativa universitaria del futuro próximo estará informatizada y será
personalizada. Además, no solamente se
evaluarán online los conocimientos teóricos, también se podrá evaluar
conocimientos prácticos, como ocurre en los Laboratorios Virtuales Inteligentes
(IVL) y será conveniente desarrollar (y, por tanto, evaluar su desarrollo)
competencias como el pensamiento crítico, las habilidades de resolución de
problemas, las habilidades de trabajo colaborativo, la comunicación, el fomento
de la innovación, la capacidad de aprender y desaprender, la creatividad y el
emprendimiento argumentando que están en la base del cambio y la introducción
de la IA en la sociedad. También se formará, y, por tanto, se evaluará, la
adquisición de conocimientos de IA aplicada al área de estudio.
En el contexto de las
tecnologías digitales fomentando un marco nuevo para la gestión de las
instituciones de educación, habrá una evaluación educativa continua con el fin
de detectar necesidades formativas. En ella, y esa es la novedad, se tendrá
especial atención a la eficacia de las interacciones entre la IA y el alumno y
las emociones en el proceso de aprendizaje online, por sus repercusiones en el
proceso de aprendizaje.
En el trabajo, Is ChatGPT helpful for
graduate students in acquiring knowledge about digital storytelling and
reducing their cognitive load? An experiment” de
Avello-Martínez, Gajderowicz y Gómez-Rodríguez (2024), se investiga el impacto
de ChatGPT en las habilidades de escritura de guiones narrativos y la carga
cognitiva. Se utiliza una muestra de 41 estudiantes de maestría inscritos en un
curso de Narrativas Digitales. Y se utiliza para ello un diseño experimental
aleatorizado.
En el estudio, como elemento
de evidencia, se utiliza un pre y un post-test para evaluar los cambios en las
habilidades de narración digital y la carga cognitiva. Los autores indicaron, a
partir de sus resultados, que no hubo una mejora significativa en las habilidades
de narración digital para el grupo experimental (que utilizó ChatGPT) en
comparación con el grupo de control, lo que sugiere que el uso de ChatGPT no
mejora notablemente las habilidades de escritura narrativa a corto plazo. Sin
embargo, se observó una reducción significativa en la carga cognitiva en el
grupo experimental, lo que apunta al potencial de ChatGPT para facilitar el
proceso de aprendizaje al reducir el esfuerzo mental requerido para la
integración y aplicación de tareas. El estudio subraya la complejidad de
integrar la IA en entornos de aprendizaje y destaca la necesidad de seguir
profundizando en estrategias para adaptar la IA a objetivos educativos
específicos. Además, señala la importancia de la investigación longitudinal
para comprender completamente los efectos a largo plazo de la IA en el
aprendizaje y el desarrollo cognitivo.
Por último, hay un ensayo, escrito
por uno de los coeditores invitados.
Se titula significativamente
AI (anthropological inquiry) on AI (artificial intelligence), es de Zvi
Bekerman (2024). Se plantea en clave de reflexión sobre el compromiso personal
del autor y la exploración de las intersecciones imprevistas entre los
paradigmas educativos tradicionales y la fuerza disruptiva de la IA.
En algún sentido el ensayo
explora espacios de uso e interpretación de la práctica con ChatGPT, y por
extensión de los LLM/IA generativa, alternativos a los que rige la convocatoria
y en alguna medida antitéticos con ella, a pesar de ser el autor coeditor y
acoautor del presente artículo editorial. Ello constituye un interesante
acicate para la discusión que en todo caso es deseable como bien mayor.
A través de esta reflexión
no se trata sólo de descubrir una herramienta tecnológica; se trata de
encontrar una nueva forma de actividad, que potencialmente podría
redefinir los contornos de la educación y el aprendizaje. Una reflexión que,
según dice, le llevó por otro lado a darse cuenta de que su interacción con
ChatGPT, marcada por un encanto inicial seguido de una fase de escrutinio
crítico, reflejaba un proceso muy humano de adquisición y validación del
conocimiento.
ChatGPT, con todas sus
capacidades y limitaciones, era, en cierto sentido, tan "humano" como
cualquiera, sigue diciendo, de sus colegas o como él mismo. El proceso de
abordar, cuestionar y validar la información que proporcionaba no fue un
testimonio de sus deficiencias, sino más bien una afirmación del enfoque
crítico y perspicaz que sustenta el trabajo académico.
Al reconocer esto, el autor
encuentra una valoración renovada en la búsqueda del conocimiento debida a la
compleja y matizada interacción entre la inteligencia humana (del latín legere
"elegir, seleccionar, leer, recopilar, reunir") y la inteligencia
artificial.
Al final el autor concluye “Estamos en una era en la que la autoría
importa, aunque tal vez hubo un momento más simple y mejor en el que no lo
hizo. Si me presionaran, no atribuiría el trabajo únicamente al chatbot o a mí.
La cuestión de la autoría tiene matices, reconociendo que ninguno de nosotros
tiene un control completo sobre los significados que expresamos, ya que los
significados siempre se interponen en alguna parte. Tal vez dejar la nota sin
atribuir sea una opción que valga la pena considerar, reconociendo la
naturaleza colaborativa de toda creación.” Observación interesante para
debatir en el contexto de las normas que se van estableciendo para referenciar
los trabajos que utilizan el socio no humano al que hemos considerado la IA
generativa.
Presentación del artículo: 30 de
enero de 2024
Fecha de aprobación: 18 de mayo de
2024
Fecha de publicación: 30 de mayo de
2024
Guàrdia Ortiz, L., Bekerman, Z., y Zapata Ros,
M. (2024). Presentación del número especial “IA generativa, ChatGPT y
Educación. Consecuencias para el Aprendizaje Inteligente y la Evaluación
Educativa”. RED. Revista de Educación a Distancia, 24(78).
http://dx.doi.org/10.6018/red.609801
Declaración de los autores sobre el uso de
LLM
Este artículo no ha utilizado textos
provenientes (o generados) de un LLM (ChatGPT u otros) para su redacción.
Financiación
Este trabajo no
ha recibido ninguna subvención específica de los organismos de financiación en
los sectores públicos, comerciales o sin fines de lucro.
Avello-Martínez, R., Gajderowicz, T.,
& Gómez-Rodríguez, V.G. (2024). Is ChatGPT helpful for graduate students in acquiring knowledge about
digital storytelling and reducing their cognitive load? An experiment. RED.
Revista de Educación a Distancia, 24(78).
http://dx.doi.org/10.6018/red.604621
Bauer, E. Greisel, M. Kuznetsov, I. Berndt,
M. Kollar, I. Dresel, M. Fischer, MR y Fischer,
F. (2023). Uso del procesamiento del lenguaje natural para
respaldar la retroalimentación entre pares en la era de la inteligencia
artificial: un marco interdisciplinario y una agenda de investigación. Revista
británica de tecnología educativa. https://doi.org/10.1111/bjet.13336
Bekerman, Z. (2024). IA (indagación
antropológica) sobre IA (inteligencia artificial). RED. Revista de Educación
a Distancia, 24(78). http://dx.doi.org/10.6018/red.609611
Biesta, G., Allan, J.,
& Edwards, R. (2011). The theory question in research capacity building in education: Towards
an agenda for research and practice. British Journal of Educational
Studies, 59(3), 225– 239.
Bond, M.,
Khosravi, H., De Laat, M., Bergdahl, N., Negrea, V., Oxley, E., ... &
Siemens, G. (2024). A meta systematic review of artificial intelligence in
higher education: a call for increased ethics, collaboration, and rigour. International
Journal of Educational Technology in Higher Education, 21(1),
4.
Chomsky, N. (2023 March 8). The False Promise of ChatGPT. The
New York Times. https://www.nytimes.com/2023/03/08/opinion/noam-chomsky-chatgpt-ai.html
Garello, M. V., & Rinaudo, M. C.
(2013). Autorregulación del aprendizaje, feedback y transferencia de
conocimiento: Investigación de diseño con estudiantes universitarios. Revista electrónica de investigación educativa, 15(2), 131-147.
Grover, S., & Pea, R. (2013). Computational thinking in K–12: A
review of the state of the field. Educational researcher, 42(1),
38-43.
Guàrdia, L., Maina, M., Cabrera, N. y
Fernández-Ferrer, N. (2024). Diseño del feedback entre pares y la
autorregulación del aprendizaje en la educación superior en línea. RED.
Revista de educación a distancia, xx (xx). http://dx.doi.org/10.6018/red.454751
Hernández-León, N. y Rodríguez-Conde,
M.J. (2024). Inteligencia artificial aplicada a la educación y la evaluación
educativa en la Universidad: introducción de sistemas de tutorización
inteligentes, sistemas de reconocimiento y otras tendencias futuras
Hwang, G. J. (2014). Definition, framework and research issues of smart
learning environments-a context-aware ubiquitous learning perspective. Smart
Learning Environments,1(1), 4. https://slejournal.springeropen.com/articles/10.1186/s40561-014-0004-5
Hilpert, J.C. , Greene, J. y Bernacki,
M. ( 2023 ). Aprovechar los marcos de complejidad
para refinar las teorías del compromiso y promover el aprendizaje autorregulado
en la era de la inteligencia artificial . Revista británica de
tecnología educativa . https://doi.org/10.1111/bjet.13340
Huh, Y., & Reigeluth, C. M. (2017).
Self-regulated learning: The
continuous-change conceptual framework and a vision of new paradigm, technology
system, and pedagogical support. Journal of Educational Technology
Systems, 46(2), 191-214.
Lorenzo Lledó, G., Lorenzo-Lledó, A., y Rodríguez-Quevedo, A. (2024). Análisis
mediante inteligencia artificial de las emociones del alumnado autista en la
interacción social con el robot NAO. RED. Revista de Educación a Distancia,
24(78). http://dx.doi.org/10.6018/red.588091
Reigeluth, C. M. (2006). New instructional theories and strategies for a
knowledge-based society. In Innovations in instructional technology (pp.
207-217). Routledge.
Reigeluth, C. M. (2016). Instructional theory and technology for the new
paradigm of education. Revista de Educación a Distancia (RED),
(50).
Ružić y Balaban (2024),The use of social robots as teaching assistants
in schools: implications for research and practice RED. Revista
de Educación a Distancia, 24(78). http://dx.doi.org/10.6018/red.600771
Wing, J. M.
(2008). Computational thinking and thinking about computing. Philosophical
Transactions of the Royal Society A: Mathematical, Physical and Engineering
Sciences, 366(1881), 3717-3725.
Zapata-Ros, M. (2013). MOOCs, una
visión crítica y una alternativa complementaria: La individualización del
aprendizaje y de la ayuda pedagógica. Campus Virtuales, 2(1),
20-38.
Zapata-Ros, M. (febrero 2014). Charles
Reigeluth: la personalización del aprendizaje y el nuevo paradigma de la
educación para la sociedad postindustrial del conocimiento. In Pensadores
de ayer para problemas de hoy: teóricos de las ciencias sociales (pp.
153-191).
Zapata-Ros, M. (2015). Teorías y
modelos sobre el aprendizaje en entornos conectados y ubicuos. Bases para
un nuevo modelo teórico a partir de una visión crítica del “conectivismo”. Education
in the Knowledge Society, 16(1), 69-102.
Zapata-Ros, M. (sept 2015). Pensamiento
computacional: Una nueva alfabetización digital. Revista de Educación a
Distancia (RED), (46).
Zapata-Ros, M. (2018). La universidad inteligente. RED.
Revista de Educación a Distancia, 57(10). http://www.um.es/ead/red/57/zapata2.pdf http://dx.doi.org/10.6018/red/57/10
Zapata-Ros, M. (Diciembre 2023).
Inteligencia Artificial y Educación ¿dónde estamos? Blog RED de Hypotheses. https://red.hypotheses.org/2607
[1] The human mind is
not, like ChatGPT and its ilk, a lumbering statistical engine for pattern
matching, gorging on hundreds of terabytes of data and extrapolating the most
likely conversational response or most probable answer to a scientific
question. On the contrary, the human mind is a surprisingly efficient and even
elegant system that operates with small amounts of information; it seeks not to
infer brute correlations among data points but to create explanations. For
instance, a young child acquiring a language is developing — unconsciously,
automatically and speedily from minuscule data — a grammar, a stupendously
sophisticated system of logical principles and parameters.
[2]
En todo caso, tal como se han definido en trabajos e investigaciones reseñadas
en las referencias, algunas de ellas aquí publicadas
[3] Estamos abiertos a una
amplia gama de tipos de contribuciones, entre las que señalamos:
·
desarrollo y prueba de una o más tecnologías particulares de
aprendizaje
·
estudios de caso de prácticas innovadoras
·
críticas a la política o la investigación
·
estudios descriptivos basados en encuestas
·
estudios longitudinales
·
experimentos empíricos
·
revisión crítica de la literatura
·
ensayos teóricos
·
proyectos de innovación o innovaciones en curso
En los casos de artículos que incluyan una o más
investigaciones solo se admite el método conocido como self-report study como método auxiliar, y en ningún caso para probar la
tesis principal del estudio.
